RAKSUL TechBlog

RAKSULグループのエンジニアが技術トピックを発信するブログです

Spike-and-Slab事前分布の概要

Technology

この記事はノバセル Advent Calendar 25日目、最終日です。

こんにちは。ノバセルでデータサイエンティストをしている石井です。
変数が重要か否かを明確化したい場面において利用することがあるSpike-and-Slab事前分布を題材として、概要をライトに書き留めます。

はじめに

Spike-and-Slab事前分布はベイズ推論において事前分布と称されるもの (詳細は後述)の一種であり、変数選択やCausalImpactの利用を通して馴染みのある分析者も一定いらっしゃるかと思います。

本論

Spike-and-Slab事前分布について6部構成で概要を記します。

1. 事前分布の役割

2. Spike-and-Slab事前分布 (縮小事前分布)とは

3. なぜSpike-and-Slab事前分布なのか

4.  ビジネス上の期待される価値

5.  重回帰分析のモデル構造

6.  推定結果の特徴

1. 事前分布の役割

主な役割は以下の通りです。

  • 過学習の抑制
    • パラメータが極端な値をとらないように抑制
  • 専門知識の反映
    • 「このパラメータはこれ程大きくはならないだろう」「正の値をとりやすい」などのドメイン知識を反映
  • 推定結果の安定化
    • サンプルサイズが少ない場合などにデータだけでは十分に推定できないパラメータを、事前分布によって安定的に推定

ベイズ推論では、事前分布による初期の仮定が、観測データから得られる情報によってアップデートされ最終的な事後分布が得られる仕組みになっています。

2. Spike-and-Slab事前分布 (縮小事前分布)とは

ベイズ推論での変数選択を得意とする事前分布の1種類であり、各回帰係数 (パラメータ) $\beta_j$の事前分布を以下の形で表現可能な混合事前分布です。


\begin{eqnarray}
\beta_j &\sim& \pi \cdot \delta_0(\beta_j) + (1 - \pi) \cdot p_{\text{slab}}(\beta_j)
\end{eqnarray}

  • $\delta_0(\beta_j)$ は $\beta_j = 0$ に点質量を持つ「スパイク」部分
  • $p_{\text{slab}}(\beta_j)$ はゼロから離れた値を許容する連続分布 (「スラブ」部分)
  • $\pi$ はスパイクとスラブの混合比率

また、上記のようにパラメータを0へと縮小する性質を持つ事前分布を縮小事前分布と呼称します。

3. なぜSpike-and-Slab事前分布なのか

馬蹄分布やLaplace分布も代表的な縮小事前分布ではあるが、以下の観点よりSpike-and-Slab事前分布を利用できることが理想的であるためです。

  • Laplace分布: 本来は重要である変数も過度に0へ縮小する傾向
  • 馬蹄分布: あくまでもSpike-and-Slab事前分布に対し連続関数で近似したもの (ただし、比較的計算コストが低い)

4. ビジネス上の期待される価値

以下の性質より「納得感のある意思決定」に資することが期待される場面があります。

① ベイズ推論の性質

  • 推定されたパラメータの不確実性を定量的に示せるため期待値コントロールを行いやすい。

② 縮小事前分布の性質

  • 重要な変数に焦点を当てることが可能であるため結果の解釈性が高い。 (セクション6 「推定結果の特徴」と繋がる話)
    • 変数が重要か否かを明確化したい場面において、Spike-and-Slab事前分布が価値を発揮する印象。(特にLaplace分布と比較した場合)

5. 重回帰分析のモデル構造

Spike-and-Slab事前分布を重回帰分析にどのように組み込めるのかをグラフィカルモデルで示します。
$\\pi$と$\\beta$により表現される$\\beta\_probabilistic$がSpike-and-Slab事前分布を用いて推定される係数です。

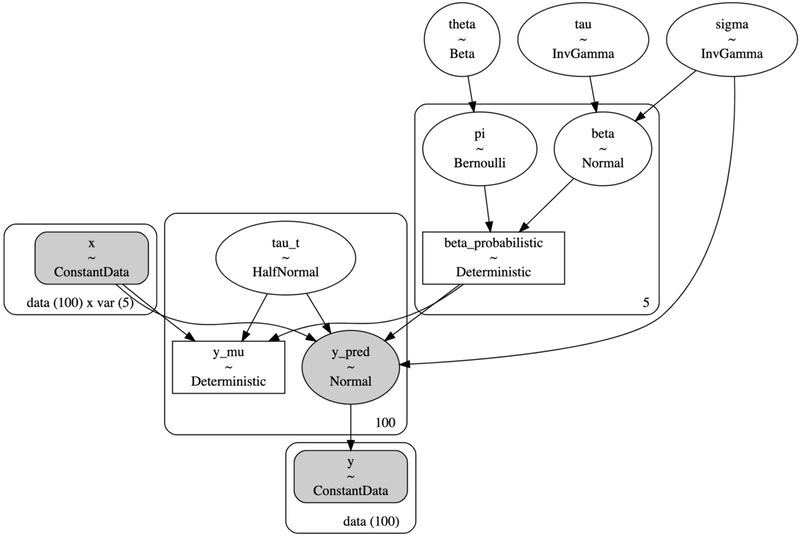
階層モデルで表現されており、以下が詳細です。

1.  指示変数 $z_j \in \{0,1\}$ を導入

  • $z_j = 1$ なら変数 $j$ は「採択」
  • $z_j = 0$ なら変数 $j$ は「非採択」

2.  指示変数 $z_j$を定義


\begin{eqnarray}
z_j &\sim& \mathrm{Bernoulli}(\pi)
\end{eqnarray}

3. $z_j$ に応じて $\beta_j$ の事前分布を切り替え


\begin{eqnarray}
\beta_j \mid z_j &=&
\begin{cases}
0, & \text{if } z_j = 0 \\
\mathcal{N}(0, \sigma^2), & \text{if } z_j = 1
\end{cases}
\end{eqnarray}

（例として「スラブ」を正規分布とした場合）

上記のように表現することで
「$z_j = 0 \Rightarrow \beta_j = 0$」
「$z_j = 1 \Rightarrow \beta_j \sim \mathcal{N}(0, \sigma^2)$」
となり、下記のようにスパイク (真に0)とスラブ (0でない連続分布)の混合を実現できます。


\begin{eqnarray}
\beta_j &=&
\begin{cases}
0, & \text{with probability } \pi \\
\text{drawn from slab distribution}, & \text{with probability } (1 - \pi)
\end{cases}
\end{eqnarray}

6. 推定結果の特徴

推定された各係数 (パラメータ)の事後分布からサンプリングした結果を示します。

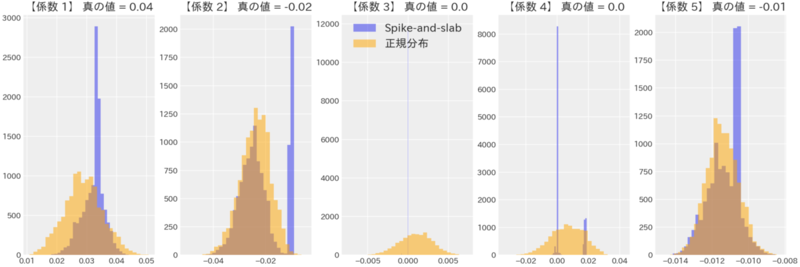
特に係数3・4の推定結果が顕著ですが、事前分布を正規分布に設定した場合と比較して、推定値が0に集中していることが見受けられます。
また、分布が定まっていない場合には、確率が最も高い、確率が60%以上のように高い確率である推定値を採択する方法を検討しても良いと思います。

おわりに

本記事では手段 (分析手法)に着目していますが、どれほど有用に思える手段から導出された結果だとしも、意思決定者に納得いただくことが先ずは重要だと考えています。
高度な手段や推定精度の向上を重視することは時に分析者のエゴであり、シンプルな手段でスピーディーにある程度の推定精度が出ており分析結果に自然な説明が付くことが、納得感のために重要であることは多々あります。
一方で納得感すらさらに先の目的を達成するための1手段でもあるため、総じて手段専攻になりすぎず、目的や障壁などを鑑みた手段を選定できる分析チームでありたい想いです。

参考資料

より深い理解を求める場合には例えばMahlet G. Tadesse, Marina Vannucci (2022). Handbook of Bayesian Variable Selection. Chapman & Hall/CRCが参考になるかと思います。